99这里精品,春色www视频在线观看,国产狂喷潮在线观看在线观看

C++掃描線思維

當前位置：點晴教程→知識管理交流 →『技術文檔交流』

freeflydom

2024年12月2日 10:15 本文熱度 678

引入

掃描線一般運用在圖形上面，它和它的字面意思十分相似，就是一條線在整個圖上掃來掃去，它一般被用來解決圖形面積，周長，以及二維數點等問題。

Atlantis 問題

題意

在二維坐標系上，給出多個矩形的左下以及右上坐標，求出所有矩形構成的圖形的面積。

解法

根據圖片可知總面積可以直接暴力即可求出面積，如果數據大了怎么辦？這時就需要講到 掃描線 算法。

過程

現在假設我們有一根線，從下往上開始掃描：

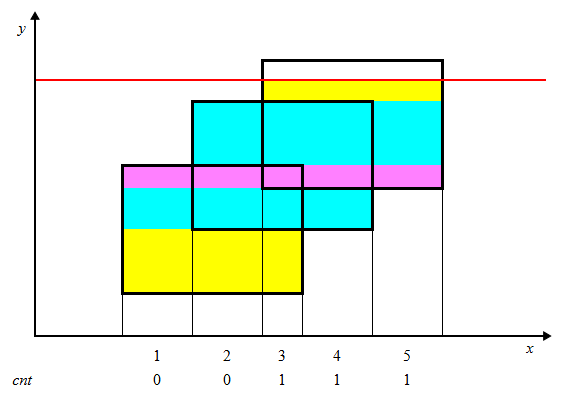
如圖所示，我們可以把整個矩形分成如圖各個顏色不同的小矩形，那么這個小矩形的高就是我們掃過的距離，那么剩下了一個變量，那就是矩形的長一直在變化。
我們的線段樹就是為了維護矩形的長，我們給每一個矩形的上下邊進行標記，下面的邊標記為 1，上面的邊標記為 -1，每遇到一個矩形時，我們知道了標記為 1 的邊，我們就加進來這一條矩形的長，等到掃描到 -1 時，證明這一條邊需要刪除，就刪去，利用 1 和 -1 可以輕松的到這種狀態。
還要注意這里的線段樹指的并不是線段的一個端點，而指的是一個區間，所以我們要計算的是 \(r+1\) 和 \(r-1\)。
需要離散化。

實現

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e5+10,mod=998244353;
typedef long long ll;
typedef pair<int,int> PII;
int T;
int n,m,k,q;
vector<array<int,4>> e;
int ans=0;
vector<int> vx;
struct info
{
    int minx,mincnt;
};
struct node
{
    info val;
    int tag;
}tr[N*8];
info operator+(const info& a, const info& b)
{
    if(a.minx<b.minx)
        return a;
    else if(b.minx<a.minx) return b;
    else
    {
        //cout<<a.mincnt<<" "<<b.mincnt<<endl;
        return (info){a.minx,a.mincnt+b.mincnt};
    }
}
void update(int p)
{
    tr[p].val=tr[2*p].val+tr[2*p+1].val;
    //cout<<p<<" "<<tr[p].val.mincnt<<endl;
}
void settag(int p,int t)
{
    tr[p].tag+=t;
    tr[p].val.minx+=t;
}
void pushdown(int p)
{
    if(tr[p].tag)
    {
        int t=tr[p].tag;
        settag(2*p,t);
        settag(2*p+1,t);
        tr[p].tag=0;
    }
}
void build(int p,int l,int r)
{
    if(l==r)
    {
        //cout<<vx[r]-vx[r-1]<<endl;
        tr[p].val={0,vx[r]-vx[r-1]};
        tr[p].tag=0;
        return ;
    }
    int mid=(l+r)/2;
    build(2*p,l,mid);
    build(2*p+1,mid+1,r);
    update(p);
    //cout<<tr[p].val.mincnt<<endl;
}
void modify(int p,int l,int r,int ql,int qr,int tag)
{
    if(l==ql&&r==qr)
    {
        settag(p,tag);
        return ;
    }
    int mid=(l+r)/2;
    pushdown(p);
    if(qr<=mid) modify(2*p,l,mid,ql,qr,tag);
    else if(ql>mid) modify(2*p+1,mid+1,r,ql,qr,tag);
    else{
        modify(2*p,l,mid,ql,mid,tag);
        modify(2*p+1,mid+1,r,mid+1,qr,tag);
    }
    update(p);
}
info query(int p,int l,int r,int ql,int qr)
{
    if(l==ql&&r==qr)
    {
        return tr[p].val;
    }
    int mid=(l+r)/2;
    pushdown(p);
    if(qr<=mid) return query(2*p,l,mid,ql,qr);
    else if(ql>mid) return query(2*p+1,mid+1,r,ql,qr);
    else return query(2*p,l,mid,ql,mid)+
    query(2*p+1,mid+1,r,mid+1,qr);
    update(p);
}
void solve()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        int x1,x2,y1,y2;
        cin>>x1>>y1>>x2>>y2;
        e.push_back({y1,1,x1,x2});
        e.push_back({y2,-1,x1,x2});
        vx.push_back(x1);
        vx.push_back(x2);
    }
    sort(e.begin(),e.end());
    sort(vx.begin(),vx.end());
    vx.erase(unique(vx.begin(),vx.end()),vx.end());
    m=vx.size()-1;
    build(1,1,m);
    //for(int i=1;i<=10;i++) cout<<tr[i].val.mincnt<<" ";
    int s=tr[1].val.mincnt;
    //cout<<s<<endl;
    int pre=0;
    int now=0;
    for(auto et : e)
    {
        int cnt=s;
        now=et[0];
        int d=tr[1].val.minx;
        //cout<<cnt<<endl;
        if(d==0) cnt-=tr[1].val.mincnt;
        ans+=(now-pre)*cnt;
        //cout<<cnt<<endl;
        pre=now;
        int x1=lower_bound(vx.begin(),vx.end(),et[2])-vx.begin()+1;
        int x2=lower_bound(vx.begin(),vx.end(),et[3])-vx.begin();
        //cout<<x1<<" "<<x2<<endl;
        if(x1>x2) continue;
        modify(1,1,m,x1,x2,et[1]);
    }
    cout<<ans<<endl;
    return ;
}
signed main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    T=1;
    //cin>>T;
    while(T--)
     {
         solve();
     }
     return 0;
}

B 維正交范圍

B 維正交范圍指在一個 B 維直角坐標系下，第 \(i\) 維坐標在一個整數范圍 \([l_i,r_i]\) 間，內部的點集。

一般來說，一維正交范圍簡稱區間，二維正交范圍簡稱矩形，三維正交范圍簡稱立方體（我們常說的二維數點就是二維正交范圍）。

對于一個靜態的二維問題，我們可以使用掃描線掃一維，數據結構維護另一維。
在掃描線從左到右掃的過程中，會在數據結構維護的那一維上產生一些修改與查詢。
如果查詢的信息可差分的話直接使用差分，否則需要使用分治。差分一般用樹狀數組和線段樹維護，但因為樹狀數組好寫而且常數小，所以大部分人會選擇用樹狀數組來維護。分治一般是 CDQ 分治（但是這里不涉及分治）。

另一種比較容易理解的看待問題的角度是站在序列角度，而不站在二維平面角度。如果我們這樣看待問題，則掃描線實際上是枚舉了右端點 \(r=1\cdots n\)，維護一個數據結構，支持查詢對于當前的 \(r\)，給定一個值 \(l\)，\(l\) 到 \(r\) 的答案是什么。即掃描線掃詢問右端點，數據結構維護所有左端點的答案，或者說遍歷一維，數據結果維護另一維。

復雜度一般為 \(O((n+m)\log n)\)。

二維數點

給一個長為 \(n\) 的序列，有 \(m\) 次查詢，每次查區間 \([l,r]\) 中值在 \([x,y]\) 內的元素個數。

這個問題就叫做二維數點。我們可以發現等價于我們要查詢一個二維平面上矩形內的點的數量和。這里講一下這個問題最簡單的處理方法，掃描線 + 樹狀數組。

很顯然，這個問題是一個靜態的二維問題，我們通過掃描線可以將靜態的二維問題轉換為動態的一維問題。維護動態的一維問題就使用數據結構維護序列，這里可以使用樹狀數組。

先將所有的詢問離散化，用樹狀數組維護權值，對于每次詢問的 \(l\) 和 \(r\)，我們在枚舉到 \(l-1\) 時統計當前位于區間 \([x,y]\) 內的數的數量 \(a\)，繼續向后枚舉，枚舉到 \(r\) 時統計當前位于區間 \([x,y]\) 內的數的數量 \(b\)，\(b-a\) 即為該次詢問的答案。

例題

洛谷 P2163[SHOI2007] 園丁的煩惱

題意：求\([x1,x2],[y1,y2]\)區間內有多少個點
思路，可以用掃描線+樹狀數組來做，按y軸從下到上掃描，同是將x坐標離散化，計算一個差分即可得出答案
代碼：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e5+10,mod=998244353;
typedef long long ll;
typedef pair<int,int> PII;
int T;
int n,m,k,q;
int a[N];
int c[N];
vector<array<int,4>> event;
int lowbit(int x)
{
    return x&(-x);
}
void modify(int p)
{
    for(;p<=N;p+=lowbit(p))
    {
        c[p]++;
    }
}
int query(int x)
{
    int res=0;
    for(;x>0;x-=lowbit(x))
    {
        res+=c[x];
    }
    return res;
}
vector<int> ans(N+1);
vector<int> vx;
void solve()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        int x,y;
        cin>>x>>y;
        vx.push_back(x);
        event.push_back({y,0,x,i});
    }
    for(int i=1;i<=m;i++)
    {
        int a,b,c,d;
        cin>>a>>b>>c>>d;
        event.push_back({d,2,c,i});
        event.push_back({d,1,a-1,i});
        event.push_back({b-1,1,c,i});
        event.push_back({b-1,2,a-1,i});
    }
    sort(event.begin(),event.end());
    sort(vx.begin(),vx.end());
    vx.erase(unique(vx.begin(),vx.end()),vx.end());
    for(auto ets : event)
    {
        if(ets[1]==0)
        {
            int id=lower_bound(vx.begin(),vx.end(),ets[2])-vx.begin()+1;
            modify(id);
        }
        else
        {
            int id=upper_bound(vx.begin(),vx.end(),ets[2])-vx.begin();
            int s=query(id);
            if(ets[1]==2) ans[ets[3]]+=s;
            else ans[ets[3]]-=s;
        }
    }
    for(int i=1;i<=m;i++) cout<<ans[i]<<"\n";
    return ;
}
signed main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    T=1;
    //cin>>T;
    while(T--)
     {
         solve();
     }
     return 0;
}

沒錯，逆序對也可以用掃描線的思維來做?？紤]將求逆序對的個數轉化為從后向前枚舉每個位置 \(i\)，求在區間 \([i+1,n]\) 中，大小在區間 \([0,a_i]\) 中的點的個數。題目中數據范圍為 \(10^9\)，很顯然要先進行離散化，我們可以考慮從后向前遍歷數組，每次遍歷到一個數時更新樹狀數組（線段樹），之后統計當前一共有多少個數小于當前枚舉的數，因為我們是從后向前遍歷的，所以比當前值小的數的個數就是他的逆序對的個數，可以用樹狀數組或線段樹進行單點修改和區間查詢。

洛谷 P1972 [SDOI2009] HH 的項鏈

簡要題意：給定一個序列，多次詢問區間 \([l,r]\) 中有多少種不同的數。

這類問題我們可以考慮推導性質，之后使用掃描線枚舉所有右端點，數據結構維護每個左端點的答案的方法來實現，我們也可以將問題轉換到二維平面上，變為一個矩形查詢信息的問題。

在本題中，我們設序列中 \(a_i\) 上一次出現的位置為 \(pre_i\)，如果 \(a_i\) 沒有出現過，則 \(pre_i = 0\)。根據題意，如果一種數在區間中出現多次，只會產生一次貢獻。不妨認為每種數產生貢獻的位置是區間中第一次出現的位置，這時可以發現，產生的總貢獻即為 \(pre_x \le l - 1\) 的個數，反證法易證。

現在問題即為：給定一個序列 \(pre\)，多次查詢區間 \([l,r]\) 中有多少個 \(pre_i \le l - 1\)。

我們可以把 \(pre_i\) 看成二維平面的點：\(i\) 是橫坐標，\(pre_i\) 是縱坐標，問題就轉化為了二維數點問題：每次詢問左下角為 \((l,0)\)，右上角為 \((r,l - 1)\) 的矩形中有幾個點。

注意到這個詢問是可差分的，我們可以將詢問差分為左下角為 \((0,0)\)，右上角為 \((r,l - 1)\) 的矩形減去左下角為 \((0,0)\)，右上角為 \((l - 1,l - 1)\) 的矩形有幾個點，這樣方便我們使用掃描線思想。

單次操作復雜度 \(O(\log n)\)，共有 \(n\) 次加點操作和 \(2m\) 次查詢操作，總時間復雜度 \(O((n + m) \log n)\)。

代碼：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+10,mod=998244353;
typedef long long ll;
typedef pair<int,int> PII;
int T;
int n,m,k,q;
vector<array<int,4>> e;
int c[N];
int a[N];
int pre[N];
int id[N];
int lowbit(int x)
{
  return x&(-x);
}
void modify(int p,int x)
{
  for(;p<=n;p+=lowbit(p))
  {
      c[p]+=x;
  }
}
int query(int x)
{
  int res=0;
  for(;x>0;x-=lowbit(x))
  {
      res+=c[x];
  }
  return res;
}
int ans[N];
void solve()
{
  cin>>n;
  for(int i=1;i<=n;i++)
  {
      cin>>a[i];
      pre[a[i]]=id[a[i]];
      e.push_back({pre[a[i]],0,i,i});
      id[a[i]]=i;
  }
  cin>>q;
  for(int i=1;i<=q;i++)
  {
      int l,r;
      cin>>l>>r;
      e.push_back({l-1,1,r,i});
      e.push_back({l-1,2,l-1,i});
  }
  sort(e.begin(),e.end());
  for(auto et : e)
  {
      if(et[1]==0)
      {
          modify(et[2],1);
      }
      else
      {
          int s=query(et[2]);
          if(et[1]==1) ans[et[3]]+=s;
          else ans[et[3]]-=s;
      }
  }
  for(int i=1;i<=q;i++) cout<<ans[i]<<endl;
  return ;
}
signed main()
{
  ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
  T=1;
  //cin>>T;
  while(T--)
   {
       solve();
   }
   return 0;
}