[點晴CRM客戶管理系統]垃圾郵件算法:貝葉斯推斷及其互聯網應用
當前位置:點晴教程→點晴CRM客戶管理信息系統
→『 經驗分享&問題答疑 』
一、什么是貝葉斯推斷 貝葉斯推斷(Bayesianinference)是一種統計學方法,用來估計統計量的某種性質。 它是貝葉斯定理(Bayes'theorem)的應用。英國數學家托馬斯·貝葉斯(ThomasBayes)在1763年發表的一篇論文中,首先提出了這個定理。  貝葉斯推斷與其他統計學推斷方法截然不同。它建立在主觀判斷的基礎上,也就是說,你可以不需要客觀證據,先估計一個值,然后根據推斷結果不斷修正。正是因為它的主觀性太強,曾經遭到許多統計學家的詬病。 貝葉斯推斷需要大量的計算,因此歷史上很長一段時間,無法得到廣泛應用。只有等到計算機誕生以后,它才獲得真正的重視。人們發現,許多統計量是無法事先進行客觀判斷的,而互聯網時代出現的大型數據集,再加上高速運算能力,為驗證這些統計量提供了方便,也為應用貝葉斯推斷創造了條件,它的威力正在日益顯現。 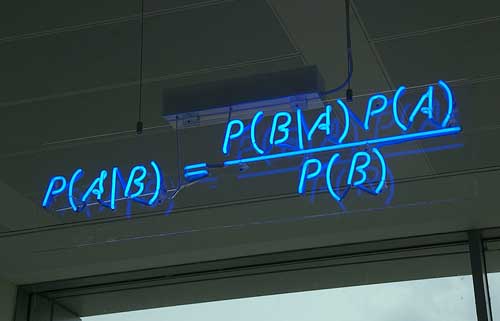 二、貝葉斯定理 要理解貝葉斯推斷,就必須先理解貝葉斯定理。后者實際上就是計算"條件概率"的公式。 所謂"條件概率"(Conditionalprobability),就是指在事件B發生的情況下,事件A發生的概率,用P(A│B)來表示。 根據文氏圖,可以很清楚地看到在事件B發生的情況下,事件A發生的概率就是P(A∩B)除以P(B)。 因此, 同理可得, 所以, 即 這就是條件概率的計算公式。 三、全概率公式 由于后面要用到,所以除了條件概率以外,這里還要推導全概率公式。 假定樣本空間S,是兩個事件A與A'的和。 上圖中,紅色部分是事件A,綠色部分是事件A',它們共同構成了樣本空間S。 在這種情況下,事件B可以劃分成兩個部分。 即 在上一節的推導當中,我們已知 所以, 這就是全概率公式。它的含義是,如果A和A'構成樣本空間的一個劃分,那么事件B的概率,就等于A和A'的概率分別乘以B的條件概率之和。 將這個公式代入上一節的條件概率公式,就得到了條件概率的另一種寫法: 四、貝葉斯推斷的含義 對條件概率公式進行變形,可以得到如下形式: 我們把P(A)稱為"先驗概率"(Priorprobability),即在B事件發生之前,我們對A事件概率的一個判斷。P(A│B)稱為"后驗概率"(Posteriorprobability),即在B事件發生之后,我們對A事件概率的重新評估。P(B│A)/P(B)稱為"可能性函數"(Likelyhood),這是一個調整因子,使得預估概率更接近真實概率。 所以,條件概率可以理解成下面的式子: 這就是貝葉斯推斷的含義。我們先預估一個"先驗概率",然后加入實驗結果,看這個實驗到底是增強還是削弱了"先驗概率",由此得到更接近事實的"后驗概率"。 在這里,如果"可能性函數"P(B│A)/P(B)>1,意味著"先驗概率"被增強,事件A的發生的可能性變大;如果"可能性函數"=1,意味著B事件無助于判斷事件A的可能性;如果"可能性函數"<1,意味著"先驗概率"被削弱,事件A的可能性變小。 五、【例子】水果糖問題 為了加深對貝葉斯推斷的理解,我們看兩個例子。 第一個例子。兩個一模一樣的碗,一號碗有30顆水果糖和10顆巧克力糖,二號碗有水果糖和巧克力糖各20顆。現在隨機選擇一個碗,從中摸出一顆糖,發現是水果糖。請問這顆水果糖來自一號碗的概率有多大? 我們假定,H1表示一號碗,H2表示二號碗。由于這兩個碗是一樣的,所以P(H1)=P(H2),也就是說,在取出水果糖之前,這兩個碗被選中的概率相同。因此,P(H1)=0.5,我們把這個概率就叫做"先驗概率",即沒有做實驗之前,來自一號碗的概率是0.5。 再假定,E表示水果糖,所以問題就變成了在已知E的情況下,來自一號碗的概率有多大,即求P(H1│E)。我們把這個概率叫做"后驗概率",即在E事件發生之后,對P(H1)的修正。 根據條件概率公式,得到 已知,P(H1)等于0.5,P(E│H1)為一號碗中取出水果糖的概率,等于0.75,那么求出P(E)就可以得到答案。根據全概率公式, 所以, 將數字代入原方程,得到 這表明,來自一號碗的概率是0.6。也就是說,取出水果糖之后,H1事件的可能性得到了增強。 六、【例子】假陽性問題 第二個例子是一個醫學的常見問題,與現實生活關系緊密。 已知某種疾病的發病率是0.001,即1000人中會有1個人得病。現有一種試劑可以檢驗患者是否得病,它的準確率是0.99,即在患者確實得病的情況下,它有99%的可能呈現陽性。它的誤報率是5%,即在患者沒有得病的情況下,它有5%的可能呈現陽性。現有一個病人的檢驗結果為陽性,請問他確實得病的可能性有多大? 假定A事件表示得病,那么P(A)為0.001。這就是"先驗概率",即沒有做試驗之前,我們預計的發病率。再假定B事件表示陽性,那么要計算的就是P(A│B)。這就是"后驗概率",即做了試驗以后,對發病率的估計。 根據條件概率公式, 用全概率公式改寫分母, 將數字代入, 我們得到了一個驚人的結果,P(A│B)約等于0.019。也就是說,即使檢驗呈現陽性,病人得病的概率,也只是從0.1%增加到了2%左右。這就是所謂的"假陽性",即陽性結果完全不足以說明病人得病。 為什么會這樣?為什么這種檢驗的準確率高達99%,但是可信度卻不到2%?答案是與它的誤報率太高有關。(【習題】如果誤報率從5%降為1%,請問病人得病的概率會變成多少?) 有興趣的朋友,還可以算一下"假陰性"問題,即檢驗結果為陰性,但是病人確實得病的概率有多大。然后問自己,"假陽性"和"假陰性",哪一個才是醫學檢驗的主要風險? 上面我們介紹了貝葉斯推斷的原理,下面講如何將它用于垃圾郵件過濾。 七、什么是貝葉斯過濾器? 垃圾郵件是一種令人頭痛的頑癥,困擾著所有的互聯網用戶。 正確識別垃圾郵件的技術難度非常大。傳統的垃圾郵件過濾方法,主要有"關鍵詞法"和"校驗碼法"等。前者的過濾依據是特定的詞語;后者則是計算郵件文本的校驗碼,再與已知的垃圾郵件進行對比。它們的識別效果都不理想,而且很容易規避。 2002年,PaulGraham提出使用"貝葉斯推斷"過濾垃圾郵件。他說,這樣做的效果,好得不可思議。1000封垃圾郵件可以過濾掉995封,且沒有一個誤判。 另外,這種過濾器還具有自我學習的功能,會根據新收到的郵件,不斷調整。收到的垃圾郵件越多,它的準確率就越高。 八、建立歷史資料庫 貝葉斯過濾器是一種統計學過濾器,建立在已有的統計結果之上。所以,我們必須預先提供兩組已經識別好的郵件,一組是正常郵件,另一組是垃圾郵件。 我們用這兩組郵件,對過濾器進行"訓練"。這兩組郵件的規模越大,訓練效果就越好。PaulGraham使用的郵件規模,是正常郵件和垃圾郵件各4000封。 "訓練"過程很簡單。首先,解析所有郵件,提取每一個詞。然后,計算每個詞語在正常郵件和垃圾郵件中的出現頻率。比如,我們假定"sex"這個詞,在4000封垃圾郵件中,有200封包含這個詞,那么它的出現頻率就是5%;而在4000封正常郵件中,只有2封包含這個詞,那么出現頻率就是0.05%。(【注釋】如果某個詞只出現在垃圾郵件中,PaulGraham就假定,它在正常郵件的出現頻率是1%,反之亦然。隨著郵件數量的增加,計算結果會自動調整。) 有了這個初步的統計結果,過濾器就可以投入使用了。 九、貝葉斯過濾器的使用過程 現在,我們收到了一封新郵件。在未經統計分析之前,我們假定它是垃圾郵件的概率為50%。(【注釋】有研究表明,用戶收到的電子郵件中,80%是垃圾郵件。但是,這里仍然假定垃圾郵件的"先驗概率"為50%。) 我們用S表示垃圾郵件(spam),H表示正常郵件(healthy)。因此,P(S)和P(H)的先驗概率,都是50%。 然后,對這封郵件進行解析,發現其中包含了sex這個詞,請問這封郵件屬于垃圾郵件的概率有多高? 我們用W表示"sex"這個詞,那么問題就變成了如何計算P(S│W)的值,即在某個詞語(W)已經存在的條件下,垃圾郵件(S)的概率有多大。 根據條件概率公式,馬上可以寫出 公式中,P(W│S)和P(W│H)的含義是,這個詞語在垃圾郵件和正常郵件中,分別出現的概率。這兩個值可以從歷史資料庫中得到,對sex這個詞來說,上文假定它們分別等于5%和0.05%。另外,P(S)和P(H)的值,前面說過都等于50%。所以,馬上可以計算P(S│W)的值: 因此,這封新郵件是垃圾郵件的概率等于99%。這說明,sex這個詞的推斷能力很強,將50%的"先驗概率"一下子提高到了99%的"后驗概率"。 十、聯合概率的計算 做完上面一步,請問我們能否得出結論,這封新郵件就是垃圾郵件? 回答是不能。因為一封郵件包含很多詞語,一些詞語(比如sex)說這是垃圾郵件,另一些說這不是。你怎么知道以哪個詞為準? PaulGraham的做法是,選出這封信中P(S│W)最高的15個詞,計算它們的聯合概率。(【注釋】如果有的詞是第一次出現,無法計算P(S│W),PaulGraham就假定這個值等于0.4。因為垃圾郵件用的往往都是某些固定的詞語,所以如果你從來沒見過某個詞,它多半是一個正常的詞。) 所謂聯合概率,就是指在多個事件發生的情況下,另一個事件發生概率有多大。比如,已知W1和W2是兩個不同的詞語,它們都出現在某封電子郵件之中,那么這封郵件是垃圾郵件的概率,就是聯合概率。 在已知W1和W2的情況下,無非就是兩種結果:垃圾郵件(事件E1)或正常郵件(事件E2)。 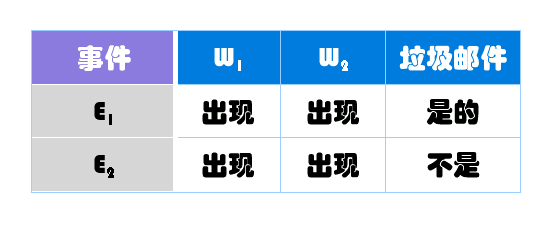 其中,W1、W2和垃圾郵件的概率分別如下:  如果假定所有事件都是獨立事件(【注釋】嚴格地說,這個假定不成立,但是這里可以忽略),那么就可以計算P(E1)和P(E2): 又由于在W1和W2已經發生的情況下,垃圾郵件的概率等于下面的式子: 即 將P(S)等于0.5代入,得到 將P(S│W1)記為P1,P(S│W2)記為P2,公式就變成 這就是聯合概率的計算公式。如果你不是很理解,點擊這里查看更多的解釋。 十一、最終的計算公式 將上面的公式擴展到15個詞的情況,就得到了最終的概率計算公式: 一封郵件是不是垃圾郵件,就用這個式子進行計算。這時我們還需要一個用于比較的門檻值。PaulGraham的門檻值是0.9,概率大于0.9,表示15個詞聯合認定,這封郵件有90%以上的可能屬于垃圾郵件;概率小于0.9,就表示是正常郵件。 有了這個公式以后,一封正常的信件即使出現sex這個詞,也不會被認定為垃圾郵件了。 該文章在 2012/6/20 1:19:06 編輯過 |
關鍵字查詢
相關文章
正在查詢... |